Gondolkodási Sémák

Vannak olyan jellegzetességei a tudat működésének, melyeket a nyelv nem zár szavakba. Az absztrakt gondolkodásban megfigyelhetőek sajátosságok, amik olyan feladatok megoldásánál jelentkeznek, ahol a feladat egyszerű, ám megoldása mégis nehéz, kontraintuitív. Egyes feladatokat az emberi tudat könnyen átlát, mások megoldása viszont valamilyen okból nehézkesnek bizonyul. Ez arra enged következtetni, hogy az adott feladatban van valami, ami a tudati működésre rosszul illeszkedik, van a feladatban valami, amit az emberi tudatnak nehéz végrehajtania. A működés részleteinek feltárása itt nem cél, a feladatok csupán annak alátámasztásául állnak itt, hogy a tudati működés jelleggel bír.

Néhány feladat, amelyek egyszerűségük ellenére mégis valahogy kifognak az emberen, megoldásuk kontraintuitív:

Valószínűségszámítási 

Szerencsejátékosok tévedése

Mi az esélye, hogy 6-ost dobunk egy fair kockával, ha előzőleg már háromszor egymás után 6-ost dobtunk? Valamiért nehezünkre esik elfogadni, hogy a múlt dobásainak kimenetelei nincsenek befolyással az aktuális dobásra, a kockadobás "örök ifjú" tulajdonságú. Hajlamos az ember kisebb valószínűségűnek gondolni az ismételt kimenetelt, mint a többit, pedig erre semmilyen racionális érv nem létezik.

Monty Hall probléma

Három elfüggönyzött nyeremény közül kell választania egy játékosnak; két kisebb és egy nagy értékű közül. Miután megtörtént a választás, az egyik nem választott kisebb értékű nyeremény elől elhúzzák a függönyt, és ilyenkor a játékos dönthet: kitart az eredeti választása mellett, vagy megváltoztatja döntését. Megdöbbentő módon, a döntés megváltoztatása jelentősen megnöveli a nagy értékű nyeremény megtalálását. A rossz választás felfedésével járó plusz információt nehezen veszi számításba a tudat, nem érezzük jelentősnek.

Logikai

Tíz érme

Tíz érme hever az asztalon, 10 fejjel, 10 írással lefelé. Az érmék vizsgálata nélkül, vakon, készítsünk két halmazt, amiben megegyezik a fejek száma! A megoldás szinte az egyetlen cselekvés, amit a feladat szabályai megengednek: két csoportra kell osztani az érméket, majd az egyik csoportban minden érmét meg kell fordítani. A feladat inkább abban áll, hogy megértsük miért működik ez a módszer.

Wason szelekciós feladat

Van 4 kártya, mindnek van egy számos és egy betűs oldala. Kettő betűvel felfelé, kettő számmal lefelé (D, F, 3, 7). Melyikeket kell megfordítani, hogy meggyőződhessünk róla, hogy a szabály, miszerint aminek D van az egyik oldalán, annak 3-as van a másikon, fennáll? A feladat érdekessége, hogy ha átfogalmazzuk egy gyakorlatiasabb környezetbe, a megoldás triviálissá válik: Kiket kell ellenőrizni egy bárban, hogy betartassuk a szabályt, miszerint mindenki aki fiatalkorú nem ihat alkoholt? Valaki sört iszik, valaki kólát, valaki fiatalkorú, valaki idős.

Fizikai

Néhány fizikai rendszer nem várt módon viselkedik, téves várakozásaink az intuíciónk hibás voltát jelzik. Van az emberekben valami közös ami azt eredményezi, hogy ugyanazokban a kérdésekben gondolkozunk helytelenül.

• Chain fountain: https://fb.watch/uOyG2RgcOd/

• Newton bölcső: https://fb.watch/uOLJ5H0_uo/ 

• Egyenletesen vízszintesen mozgó helikopterből kilógatott kötél alakja:

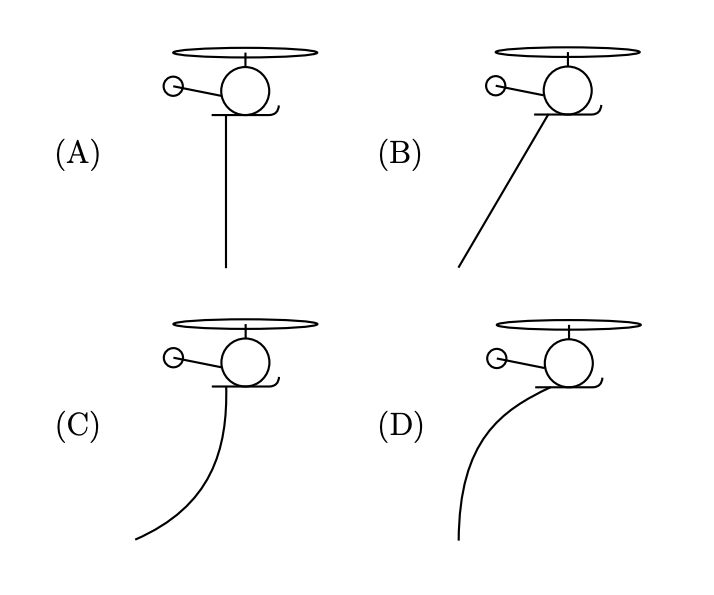
A felsorolt példák azt igyekeznek alátámasztani, hogy a gondolkodásunk mélyén olyan tökéletlen mechanizmusok dolgoznak, amik bizonyos feladatokra kevésbé alkalmasak, mint másokra, és ez a különbség nem egyszerűen a feladatok méretéből, vagy komplexitásából adódik, hanem magának a gondolkozás folyamatának jellegéből.